Die Poker Mathematik und die korrekte Berechnung von Poker Chancen ist ein entscheidender Faktor für Ihren Gewinn oder Niederlagen. Bei Live Events im TV ist häufig die Rede von „Bauchgefühl“. Doch die Realität sieht meist ganz anders aus. Impulsive und mathematisch falsche Entscheidungen können auf Dauer zu gravierenden Verlusten führen.
Die größte Fehlerquelle ungeübter Spieler sind emotionale Entscheidungen. Insbesondere, wenn es über einen langen Zeitraum nicht gut läuft oder Sie keine guten Hände erhalten und Ihre Gegenspieler im rechten Moment die unwahrscheinlichsten Hände gegen Sie legen, laufen Sie Gefahr, aus der Emotion heraus falsche Entscheidungen zu treffen.
Das Beherrschen der Poker Mathematik bedeutet ein tiefes Verständnis des Pokerspiels, wodurch Sie mehr Kontrolle über Ihre Emotionen erlangen. Zur Mathematik des Pokers gehört auch das Wissen, dass Sie im Durchschnitt über 200 Spielrunden auf ein Paar Asse warten müssen. Gegen drei weitere Spieler haben Sie damit nur rund 65 % Gewinnchance.
Das Pokerspiel besteht aus 52 Karten; aus denen sich grundsätzlich immer mathematische Möglichkeiten ergeben. In diesem Artikel werden wir uns in erster Linie mit der Mathematik des Texas Hold’em Poker beschäftigen, da diese Variante besonders beliebt ist. Viele mathematische Grundregeln sind aber auch auf andere Pokervarianten übertragbar.
| Texas Hold’em |
| Beim Texas Hold’em erhalten Sie zu Spielbeginn zwei Karten auf die Hand, die sogenannten Holecards. Danach teilt der Dealer die ersten drei Gemeinschaftskarten aus, den sogenannten Flop, gefolgt von den einzelnen Karten Turn und River. Insgesamt befinden sich am Ende einer solchen Spielrunde bis zu fünf offene Gemeinschaftskarten auf dem Tisch, ergänzt durch Ihre zwei Holecards, mit denen Sie die beste Fünf-Karten-Hand bilden. |
Um Ihnen einen ersten Überblick zu verschaffen, erklären wir Ihnen zunächst die Wertigkeit und Reihenfolge der Poker Hände. Dazu beginnen wir mit der stärksten Kombination im Poker – dem berühmten Royal Flush:
Hand-Reihenfolge
- Royal Flush: Die höchste Hand im Poker (A-K-Q-J-10 der gleichen Farbe).
- Straight Flush: Fünf aufeinanderfolgende Karten der gleichen Farbe.
- Vierling: Vier Karten des gleichen Rangs (z. B. 4 Asse).
- Full House: Ein Drilling und ein Paar (z. B. 3 Asse und 2 Könige).
- Flush: Fünf Karten der gleichen Farbe, aber nicht aufeinanderfolgend.
- Straight: Fünf aufeinanderfolgende Karten, unabhängig von der Farbe.
- Drilling: Drei Karten des gleichen Rangs (z. B. 3 Asse).
- Zwei Paare): Zwei Kartenpaare (z. B. 2 Asse und 2 Könige).
- Paar: Zwei Karten des gleichen Rangs (z. B. 2 Asse).
- Hohe Karte: Keine Kombination – die höchste Karte entscheidet.
Basierend auf den fünf Gemeinschaftskarten und der Kombination mit Ihren zwei Holecards gibt es eine statistische Wahrscheinlichkeit, wie häufig Sie diese Kartenkombinationen erhalten können:
| Hand | Wahrscheinlichkeit (%) | Eine Hand von |
| Royal Flush | 0,000154 % | 1 von 649.740 |
| Straight Flush | 0,00139 % | 1 von 72.193 |
| Vierling | 0,0240 % | 1 von 4.165 |
| Full House | 0,1441 % | 1 von 693 |
| Flush | 0,197 % | 1 von 508 |
| Straight | 0,3925 % | 1 von 255 |
| Drilling | 2,1128 % | 1 von 47 |
| Zwei Paare | 4,7539 % | 1 von 21 |
| Ein Paar | 42,2569 % | 1 von 2,37 |
| Hohe Karte | 50,1177 % | 1 von 2 |
Im Umkehrschluss bedeuten diese Werte, dass Sie tatsächlich in den meisten Fällen keine Kombination erhalten. Gegen einen oder mehrere Gegner gewinnen Sie oft mit einer hohen Karte und es kommt eher selten zu einem Showdown.
Doch gerade, weil Sie beispielsweise so selten einen Flush oder ein Full House erhalten, trüben diese vermeintlich starken Hände häufig den Blick vor der potentiellen Stärke der Hände Ihrer Gegner. Darauf werden wir weiter unten noch genauer eingehen.
Poker Mathematik: Wahrscheinlichkeit
Als nächstes möchten wir Ihnen die Poker Wahrscheinlichkeit der stärksten Starthände aufzeigen und Ihnen damit verdeutlichen, warum viele Spieler viel zu häufig in den Pot involviert sind. Außerdem sollten Sie wissen, was das für Sie schlussendlich bedeuten kann.
| Starthand | Wahrscheinlichkeit (%) | Eine Hand von |
| Asse (A-A) | 0,4525 % | 1 von 221 |
| Könige (K-K) | 0,4525 % | 1 von 221 |
| Paar Damen (Q-Q) | 0,4525 % | 1 von 221 |
| Ass-König Suited (A-Ks) | 0,301 % | 1 von 332 |
| Paar Buben (J-J) | 0,4525 % | 1 von 221 |
| Paar Zehnen (10-10) | 0,4525 % | 1 von 221 |
| Ass-Dame Suited (A-Qs) | 0,301 % | 1 von 332 |
| Ass-König Offsuit (A-Ko) | 0,904 % | 1 von 110 |
| Ass-Bube Suited (A-Js) | 0,301 % | 1 von 332 |
| König-Dame Suited (K-Qs) | 0,301 % | 1 von 332 |
Poker Mathematik: Wahrscheinlichkeit berechnen
Solche Tabellen finden Sie Online zuhauf. Jedoch erklären Ihnen die meisten Poker Seiten dabei nicht, wie genau solche Zahlen entstehen. Daher werden wir Ihnen mit ein paar Beispielen die Berechnung dieser Prozentsätze näherbringen.
Beispiel 1: Asse (AA)
Beim Poker gibt es insgesamt 52 Karten. Für eine bestimmte Starthand, wie AA, gilt folgende Überlegung: Es gibt 4 Asse im Deck. Die Wahrscheinlichkeit, dass die erste Karte ein Ass ist, berechnet sich ganz einfach, indem Sie die vier Asse durch die 52 Spielkarten teilen:
4/52≈7,6923 %
Da Sie direkt mit der ersten Karte ein Ass erhalten haben, bleiben noch 51 Karten im Deck. Darunter drei weitere Asse. Um mit Ihrer zweiten Karte das zweite Ass zu bekommen, teilen Sie die drei verbleibenden Asse durch die verbleibenden 51 Karten:
3/51≈5,8824 %
Um nun die gesamte Wahrscheinlichkeit, zwei Asse als Starthand zu erhalten, zu berechnen, multiplizieren Sie die beiden Wahrscheinlichkeiten:
(4/52)×(3/51)=12/2652≈0,4525 %
Alternativ können Sie die Chance für die Starthand auch wie folgt ausrechnen:
Zunächst müssen Sie die möglichen Ass-Kombinationen berechnen. Das bedeutet: Vier Asse befinden sich im Deck und Sie benötigen zwei davon. Da es beim Poker nur vier Karten pro Wertigkeit gibt, ist die Berechnung des Binomialkoeffizienten nicht allzu kompliziert:
(4×3)/(2×1)=12/2 = 6 mögliche Kombinationen
Diese Kombinationen lauten:
- Ah-As (Ace of Hearts und Ace of Spades)
- Ah-Ad (Ace of Hearts und Ace of Diamonds)
- Ah-Ac (Ace of Hearts und Ace of Clubs)
- As-Ad (Ace of Spades und Ace of Diamonds)
- As-Ac (Ace of Spades und Ace of Clubs)
- Ad-Ac (Ace of Diamonds und Ace of Clubs)
Wir schreiben hier bewusst auf Englisch, da diese Kürzel in den meisten Poker-Softwares so verwendet werden.
- Hearts (h) = Herz
- Spades (s) = Pik
- Diamonds (d) = Karo
- Clubs (c) = Kreuz
Im Spiel gibt es (52 × 51) / (2 × 1) = 2.652 / 2 = 1.326 mögliche Kombinationen. Diese Zahl bleibt für die Starthände grundsätzlich gleich.
Unter dem Strich kommen Sie aber auf den gleichen Wert wie oben. Die Wahrscheinlichkeit, AA als Starthand zu bekommen, ist also:
6/1.326≈0,0045249
Multipliziert mit 100, um den Prozentwert zu erhalten:
0,0045249×100≈0,4525%
Beispiel 2: Ass-König (AK)
Als nächstes werden wir die Poker Wahrscheinlichkeit für die ebenfalls äußerst beliebte Starthand Ass-König berechnen. Die Poker Mathematik gleicht der Berechnung oben, da Sie zunächst ein Ass aus den 52 Karten benötigen.

Die Berechnung mit zwei verschiedenen Karten ist etwas einfacher. Es gibt 16 mögliche AK-Kombinationen – dank der vier Asse und vier Könige im Spiel:
4×4=16
Daraus ergibt sich:
16/1.326≈0,01206×100=1,206 %
Für die detaillierte Berechnung:
=4/52≈7,6923 %
=4/51≈7,8431 %
=(4/52)×(4/51)=16/2.652≈0,603 %
Sollten Sie sich wundern, warum das Ergebnis nur die Hälfte beträgt, liegt es daran, dass hier auch die Reihenfolge berücksichtigt wird. Sie erhalten also zuerst das Ass und dann der König. Sie müssen jedoch auch die Reihenfolge König-Ass berücksichtigen:
P(AK oder KA)=2×(4/52)×(4/51)=1,206 %
Diese Mathematik für Poker kann auf den ersten Blick sehr kompliziert und verwirrend wirken. Die Nutzung einer Tabelle ist wesentlich leichter und schneller. Wir wollten Ihnen jedoch zeigen, wie Sie vorgehen müssen, wenn Sie selbst Poker Wahrscheinlichkeiten berechnen möchten.
Bereits an diesem ersten Beispiel wird deutlich, wie tiefgreifend und wichtig die Poker Mathematik für die grundlegende Struktur des Spiels ist. Auf dem Weg zum Poker-Profi kommen Sie an dieser Basis nicht vorbei.
| Spieltipp |
| Gerade an Pokertischen mit relativ kleinen Einsätzen, egal ob Turniere, Sit-and-Goes oder Cash-Tables, finden Sie häufig Spieler, die fast jede zweite Hand spielen – weil sie einfach die Action lieben und nicht abwarten können. Wie Sie sich jetzt schon denken können, müssen Sie im Poker auch einiges an Geduld beweisen, da Sie sicherlich nicht jede Hand spielen sollten. Wie selten die starken Hände auftauchen, wissen Sie nun. |
Diesen Zusammenhang möchten wir Ihnen nun anhand einiger weiterer interessanter Kombinationen und deren Wahrscheinlichkeiten verdeutlichen:
| Starthand | Anzahl möglicher Kombinationen | Wahrscheinlichkeit (%) |
| Paare (z. B. AA, KK, 22) | 78 | 5,88 % |
| Zwei verschiedene Karten (z. B. AK) | 936 | 72,53 % |
| Gleichfarbige Karten (z. B. AKs) | 312 | 23,53 % |
| Offsuited Karten (z. B. AKo) | 624 | 46,80 % |
| Jede Hand | 1326 | 100 % |
Zur Berechnung der Prozente müssen Sie die Gesamtzahl möglicher Kombinationen der Starthände berücksichtigen: 1.326. Für Paare gilt also:
78/1.326=5,88 %
Generell sollten Sie beachten, dass Sie auch mit den besten Starthänden nicht immer gewinnen. Spätestens mit den Gemeinschaftskarten ergeben sich weitere mathematische Möglichkeiten.
All diese Regeln gelten auch für Ihre Konkurrenten. Behalten Sie das stets im Blick. Denn sobald Sie die Poker Mathematik beherrschen, sollten Sie Ihr Augenmerk auf Ihre Gegner richten – und nicht mehr nur auf Ihr Blatt.
Poker Odds und Outs
In diesem Abschnitt behandeln wir die Poker Begrffe Pot Odds, Poker Outs und weitere Konzepte. Grundsätzlich zeigen die Pot Odds die mathematische Wahrscheinlichkeit, wie sich Ihre zwei Holecards auf dem Flop (den ersten drei Gemeinschaftskarten) und im späteren Verlauf auf dem Turn und River verbessern.
Achtung: Hier geht es ausschließlich um die mathematische Wahrscheinlichkeit, eine bestimmte Kombination zu treffen und nicht um den erwarteten möglichen Gewinn. Punkte wie Expected Value (erwarteter Wert) besprechen wir später.
Was sind Outs?
Outs sind Karten im Deck, die Ihre Hand potenziell verbessern.
Halten Sie beispielsweise zwei Asse in der Hand, können Sie auf ein Drilling (Triple) hoffen, also das dritte Ass. In diesem Beispiel haben Sie zwei Outs, da von den insgesamt vier Assen noch zwei im Deck sind. Fakt ist:
- Es gibt 4 Asse im Deck.
- Sie halten bereits 2 Asse.
- Die verbleibenden Asse sind Ihre Outs.
Outs=4−2=2
Oder Sie spekulieren auf einen Flush, da Sie zwei Herzkarten in der Hand halten. Insgesamt gibt es 13 Herzkarten in einem Kartendeck. Da Sie bereits zwei Herzkarten auf der Hand haben, verbleiben noch 11 Herzkarten im Deck. Wenn der Dealer auf dem Flop (den ersten drei Gemeinschaftskarten) zwei weitere Herzkarten ausgibt, sind noch 9 Herzkarten im Deck. In diesem Fall hätten Sie auf dem Turn noch 9 Outs, um Ihren Flush zu vervollständigen.
- Es gibt 13 Karten einer Farbe.
- Sie halten 2 Herzkarten auf der Hand, 2 weitere befinden sich auf dem Board.
- Die verbleibenden Herz-Karten sind also:
Outs=13−4=9
Was sind Odds?
Auf Grundlage der Outs können Sie nun die entsprechenden Odds berechnen, also die mathematische Poker-Wahrscheinlichkeit, Ihre Hand zu verbessern. Als Grundlage dient immer das klassische 52-Kartendeck.

Odds = Karten, die Ihre Hand nicht verbessern / Karten, die Ihre Hand verbessern
Das Beispiel mit den Outs oben diente zur Veranschaulichung. Die eigentliche Odds-Berechnung wird erst ab dem Austeilen der Gemeinschaftskarten relevant. Dazu nutzen wir erneut den Flush als Beispiel. Hier haben Sie eine relativ hohe Chance, den Flush zu treffen. Die Berechnung sieht wie folgt aus:
- Sie halten zwei Herzkarten auf der Hand und zwei weitere befinden sich auf dem Flop. Insgesamt kennen Sie also 5 der 52 Karten. Somit bleiben 47 unbekannte Karten im Deck.
- Es gibt insgesamt 13 Herzkarten, wovon Sie bereits 4 kennen. Es verbleiben also 9 Herzkarten im Deck.
Das bedeutet: Von den verbleibenden 47 Karten helfen Ihnen 9 Karten weiter, 38 Karten nicht (47 – 9 = 38).
Somit bleiben 9 Karten, die Ihnen helfen, und 38 Karten, die keinen Wert für Sie besitzen. Damit können Sie das Verhältnis (die Odds) berechnen:
Odds = 38 / 9 ≈ 4,22
Das bedeutet also, dass Sie in etwa einem von vier Fällen den Flush mit der nächsten Gemeinschaftskarte (Turn oder River) vervollständigen.
Rule of 2 and 4
Die Berechnung der Odds am Pokertisch – und das möglicherweise in Sekundenbruchteilen – ist natürlich schwierig. Glücklicherweise gibt es einen kleinen Trick, der sich „Rule of 2 and 4“ nennt. Zwar stimmen die Werte nicht exakt mit den mathematisch korrekten Wahrscheinlichkeiten überein, aber sie sind nahe genug an der Realität, um sie effektiv im Spiel nutzen zu können.
Die Regel lautet:
- Multiplizieren Sie Ihre Outs nach dem Flop mit 4.
- Multiplizieren Sie Ihre Outs nach dem Turn mit 2.
Beispiel:
Outs für einen Flush: 9 Karten.
Mathematische Poker-Wahrscheinlichkeit auf den Flush:
- Nach dem Flop: 9 × 4 = 36 %.
- Nach dem Turn: 9 × 2 = 18 %.
Zum Vergleich die korrekte mathematische Berechnung:
Mit zwei verbleibenden Karten (Turn und River):
(Outs×2)/verbleibende Karten im Deck=(9×2)/47=18/47≈38,3 %
Mit einer verbleibenden Karte (nur River):
(Outs×1)/verbleibende Karten im Deck=(9×1)/46=9/46≈19,57 %
Wie Ihnen vielleicht bereits aufgefallen ist, weichen die Prozentzahlen leicht von den exakten Werten ab. Um dies zu korrigieren, gibt es einen weiteren Trick:
- Addieren Sie nach dem Flop 2.
- Addieren Sie nach dem Turn 1.
Somit ergibt sich eine neue Faustformel.
Beispiel:
Outs für einen Flush: 9 Karten.
Mathematische Poker-Wahrscheinlichkeit auf den Flush:
- Nach dem Flop: 9 × 4 + 2 = 38 %.
- Nach dem Turn: 9 × 2 + 1 = 19 %.
| Merken Sie sich also diese Regel |
|
Poker Odds and Outs Beispiele
Da Sie nun wissen, was Outs sind und wie Sie die Odds berechnen, möchten wir Ihnen noch eine Tabelle mit den wahrscheinlichsten Szenarien an die Hand geben. Diese Szenarien treten so häufig auf, dass es sich lohnt, die folgenden Odds und Outs auswendig zu lernen:
| Outs | Odds – Flop bis Turn | Odds – Flop bis River | Beispiel |
| 2 | 22:1 | 11:1 | Kleineres Paar gegen höheres Paar |
| 3 | 15:1 | 7:1 | Eine Overcard |
| 4 | 10:1 | 5:1 | Gutshot Straight Draw |
| 6 | 7:1 | 3:1 | Zwei Overcards |
| 8 | 5:1 | 2:1 | Straight Draw (open-ended) |
| 9 | 4:1 | 2:1 | Flush Draw |
| 12 | 3:1 | 1,2:1 | Gutshot und Flush Draw |
| 15 | 2:1 | 1:1 | Flush Draw plus Straight Draw |
Profi Mathematik
Sie können nun Ihre Outs und Ihre exakten Chancen auf ein bestimmtes Blatt berechnen. Doch jetzt kommt der Faktor X ins Spiel. Sie sollten grundsätzlich immer im Auge behalten, welche Blätter Ihre Gegenspieler auf der Hand halten könnten. Hier sollten Sie auch einkalkulieren, welchen Gewinn Sie potentiell erzielen können – im Verhältnis zu Ihren Einsätzen.
Pot Odds
Sie wissen nun, wie hoch Ihre Chancen sind, zum Beispiel mit einem Flush Draw auf dem Turn oder River diese Hand zu vervollständigen und damit vermutlich Ihre Gegenspieler zu schlagen. Jetzt kommen die Pot Odds ins Spiel, die Sie sowohl für sich nutzen können als auch beachten müssen, wenn Ihre Gegenspieler Sie unter Druck setzen.
Die Pot Odds berechnen sich wie folgt:
Pots = Betrag im Pott / zu bringender Einsatz
Beispiel:
Die Chance, Ihren Flush Draw mit 9 Outs auf dem Turn zu treffen, liegt bei ca. 19 %. Der aktuelle Pot beträgt 8 €, und der Gegenspieler setzt 2 €. Der gesamte Pot beträgt jetzt 10 €. Daraus ergeben sich folgende Pot Odds:
Pot Odds = 10/2 = 5 = 5:1
In Prozent: ⅙x100 = 16,67 %
Das bedeutet, Sie müssten 16,67 % des Pots bezahlen, aber Ihre Chance, den Flush zu vervollständigen, liegt bei 19 %. Somit wäre ein Call profitabel.
Alternativ können Sie auch einen entsprechenden Einsatz machen, um den Pot zu vergrößern. Mathematisch wäre das korrekt, auch wenn kein Einsatz natürlich die günstigere Lösung wäre. Allerdings müssen Sie in die Zukunft schauen und bedenken: Wenn Sie Ihren Flush treffen und der Pot groß genug ist, wäre ein weiterer Einsatz für Ihren Gegner zu verlockend – und er bezahlt Sie somit!
Damit kommen wir nun auch schon zu den Impliziten Odds.
Implied Odds
Bei den Implied Odds kommt natürlich etwas Spekulation hinzu. Implied Odds bedeuten eine Erweiterung der Pot Odds. Hier berücksichtigen Sie nicht nur die mathematisch korrekten Chancen. Sie helfen Ihnen auch dabei, die Situation besser einzuschätzen und Ihren möglichen Profit zu maximieren.
Implied Odds können ungünstige Pot Odds in günstige verwandeln. Die Formel lautet:
Implied Odds = möglicher zukünftiger Gewinn / zu setzender Betrag
Beispiel:
Sie halten erneut den 9-Outs-Flush-Draw, mit einer 19%igen Chance, diesen auf dem Turn zu treffen und einer 38%-igen Chance bis zum River.
Der aktuelle Pott beträgt 8 €, und Ihr Kontrahent setzt 4 €. Der Pot liegt nun bei 12 €, und Ihre Pot Odds betragen:
Pot Odds = 12/4 = 3 = 3:1
In Prozent ¼ x100 = 25 %
In der Theorie übersteigt der zu bringende Einsatz (25 %) die 19%ige Chance, Ihre Hand auf dem Turn zu verbessern. Jetzt kommen die Implied Odds ins Spiel.
Sie rechnen damit, dass Ihr Gegner auf einer starken Hand sitzt oder sich schwer damit tut, eine Hand aufzugeben. Aufgrund Ihrer Erfahrung gehen Sie davon aus, dass Sie mindestens weitere 8 € bis zum Showdown von ihm erwarten können. Die neue Berechnung lautet:
Implied Odds = (12+8) 4 = 5 = 5:1
In Prozent ⅙x100 = 16,67 %
Mit den zusätzlichen erwarteten Einsätzen und der Berechnung der Implied Odds sehen Sie nun einem positiven Ergebnis entgegen.
Reverse Implied Odds
Reverse Implied Odds sind ein ähnlicher Fall, wie die Implied Odds – jedoch mit einem negativen Verlauf. Die Reverse Implied Odds berücksichtigen, dass Ihr Gegenspieler möglicherweise eine noch stärkere Hand hält, als ein Full House, das Ihren Flush schlagen würde. In diesem Fall wäre die oben genannte Hand mit einem Flush nicht profitabel.
Erfahrene Poker Profis blicken meist jedoch mit Skepsis auf Reverse Implied Odds. Sie können zwar eintreten, führen aber oft dazu, dass Sie mehr verschenken, wenn Sie aufgrund des Verdachts eine starke Hand aufgeben. Eine Ausnahme wäre, wenn mehrere Gegenspieler noch im Pot sind und auch bei hohen Einsätzen niemand bereit ist, seine Hand aufzugeben.
Expected Value (EV)
Der Expected Value (EV) setzt sich aus der Gewinnwahrscheinlichkeit und dem möglichen Gewinnbetrag sowie der Verlustwahrscheinlichkeit und dem dementsprechenden Verlustbetrag zusammen. Die Formel lautet:
EV=(Gewinnwahrscheinlichkeit×Gewinnbetrag)−(Verlustwahrscheinlichkeit×Verlustbetrag)
Besonders gut lässt sich dies anhand unseres bereits bekannten Flush Draw Beispiels mit 9 möglichen Outs erklären. Dieses Mal rechnen wir jedoch mit den exakten Prozentzahlen.
- Die Gewinnwahrscheinlichkeit, den Flush auf dem Turn zu vervollständigen, liegt bei: 9/47≈19,15 %
- Die Verlustwahrscheinlichkeit entsprechend bei: 1-9/47≈80,85 %
EV-Berechnung:
- Pot wie im ersten Beispiel: 8 €
- Zu bringender Einsatz: 2 €
- Gewinnwahrscheinlichkeit: 19,15 %
- Verlustwahrscheinlichkeit: 80,85 %
Die EV-Berechnung lautet: EV=(Gewinnwahrscheinlichkeit×Gewinnbetrag)−(Verlustwahrscheinlichkeit×Verlustbetrag)
= EV=(0,1915×10)−(0,8085×2)=0,298€
In diesem Fall beträgt der Expected Value rund 30 Cent. Das bedeutet, dass dieser Zug langfristig profitabel ist.
Die Berechnung des Expected Value liefert vor allem langfristig nützliche Informationen und wird in einigen Tools verwendet, um zu analysieren, ob Sie in bestimmten Situationen gewinn- oder verlustbringende Entscheidungen treffen. Der EV bietet sich besonders zu Analysezwecken an. Weiter unten stellen wir Ihnen noch entsprechende Software vor.
Die Poker Varianz
Im Grunde kennen Sie nun die fundamentalen Aspekte der Poker Mathematik. Wir möchten jedoch noch gesondert auf den Faktor „Glück“ eingehen, der auch als Poker-Varianz bezeichnet wird. Denn auch, wenn Poker primär als Geschicklichkeitsspiel gilt, spielt die Varianz eine große Rolle.
Beim Pokerspiel gibt es viele verschiedene Varianten und einige von ihnen haben eine deutlich höhere Poker-Varianz. Diese zwingen Sie und Ihre Gegenspieler dazu, risikoreicher zu spielen. Dadurch wird die Poker Varianz automatisch erhöht.
Solche Varianten finden Sie hauptsächlich in Turnieren oder Sit & Go Turnieren. Der Grund dafür ist die Geschwindigkeit, mit der die Blinds ansteigen. Dadurch zwingt Sie das Spiel, häufiger Hände zu spielen, die Sie unter normalen Umständen vielleicht eher nicht spielen würden.
| Independent Chip Model (ICM) |
| Hier kommt das äußerst interessante und zugleich komplexe Independent Chip Model (ICM) ins Spiel. Dieses Modell berechnet, wie viel Ihre aktuellen Chips im Vergleich zu den möglichen Preisen wert sind. Das ICM hilft Ihnen, auf mathematischer Ebene zu entscheiden, wann Sie in einem Turnier bei steigenden Blinds All-in gehen sollten oder nicht.
Es gibt zwar Anfängerartikel zum Thema ICM, jedoch ist dieses Thema ein absolutes Profi-Gebiet. Falsche Berechnungen können Sie mehr Geld kosten, als es Ihnen bringt. Möchten Sie aber langfristig ein profitabler Poker Spieler im Turnier- oder Sit & Go-Bereich sein, kommen Sie um ICM nicht herum. Das Thema hier im Detail zu erklären, würde allerdings den Rahmen sprengen. |
Mit steigenden Blinds wächst auch die Notwendigkeit, häufiger All-in zu gehen. In der folgenden Tabelle erhalten Sie einen groben Überblick darüber, was passiert, wenn Sie mit einer bestimmten Hand All-in gehen und wie Ihre Poker Chancen stehen.
| Showdown | Wahrscheinlichkeiten |
| AK vs. 89 | 60 % für AK |
| AQ vs. 76 | 65 % für AQ |
| KQ vs. JTs | 55 % für KQ |
| AA vs. KK | 82 % für AA |
| JJ vs. AKo | 57 % für JJ |
| TT vs. 55 | 81 % für TT |
| 88 vs. A7o | 68 % für 88 |
| QJs vs. 65s | 61 % für QJs |
| AK vs. QJ | 64 % für AK |
| AKo vs. T9s | 60 % für AKo |
Wie Sie sehen, sind Sie mit einigen vermeintlich starken Händen gar nicht immer der große Favorit. Letzten Endes können Sie langfristig immer die mathematisch korrekten Entscheidungen treffen und trotzdem kurz- oder mittelfristig Verluste machen.
Bedenken Sie etwa den normalen Münzwurf, der Ihnen eine 50/50-Chance auf Kopf oder Zahl bietet. Wenn Sie die Münze 10 Mal werfen, könnte es sein, dass 2-mal Kopf erscheint und 8-mal Zahl. Werfen Sie die Münze 100 Mal, könnten es 40 Mal Kopf und 60 Mal Zahl sein.
Doch je öfter Sie die Münze werfen, desto näher wird das Ergebnis an die 50/50-Verteilung herankommen. Werfen Sie die Münze 1.000 Mal, ist die Wahrscheinlichkeit hoch, dass Sie deutlich näher an das tatsächliche 50/50-Ergebnis herankommen.
Beispiel 1: 10 Münzwürfe
20 % Kopf, 80 % Zahl (2-mal Kopf, 8-mal Zahl).
Beispiel 2: 100 Münzwürfe
40 % Kopf, 60 % Zahl (40-mal Kopf, 60-mal Zahl).
Beispiel 3: 1.000 Münzwürfe
49 % Kopf, 51 % Zahl (490-mal Kopf, 510-mal Zahl).
Wie Sie am Münzwurf-Beispiel erkennen, gleicht sich die Varianz im Laufe des Spiels aus. Jedoch sollten Sie beim Poker spielen immer mit sogenannten Downswings und Upswings rechnen.
Downswings können einen doppelt negativen Effekt erzeugen. Zum einen verlieren Sie Geld, zum anderen verunsichern Downswings den Spieler häufig. Insbesondere Anfänger, auch wenn sie gut spielen, geraten in solchen Phasen oft in einen fatalen Abwärtstrend.
Sie passen ihr eigentlich gutes Spiel an, lassen sich von den Verlusten beeinflussen und treffen unbewusst schlechtere Entscheidungen. Um das zu verhindern, helfen Ihnen sogenannte Poker-Tools. Diese liefern Statistiken und geben Ihnen ein objektives Zeugnis über Ihr Spiel.
Poker Mathematik Software
Beherrschen Sie die Grundlagen und die fundamentale Pokermathematik, stehen Sie an der Schwelle zu profitablem Poker. Um diese Schwelle zu überschreiten, sollten Sie tiefer in die Materie einsteigen. Dabei helfen Ihnen verschiedene kostenpflichtige Programme wie der PokerTracker.
![]()
Der PokerTracker zeichnet Ihr Spiel auf und Sie können anhand dieser Daten verschiedene Analysen starten. Insbesondere können Sie sehen, wie stark Sie in den jeweiligen Positionen spielen oder ob Sie generell die richtigen Entscheidungen treffen. So erkennen Sie schnell, ob Sie Ihre Asse überspielen oder in zu viele verlustreiche Hände involviert sind.
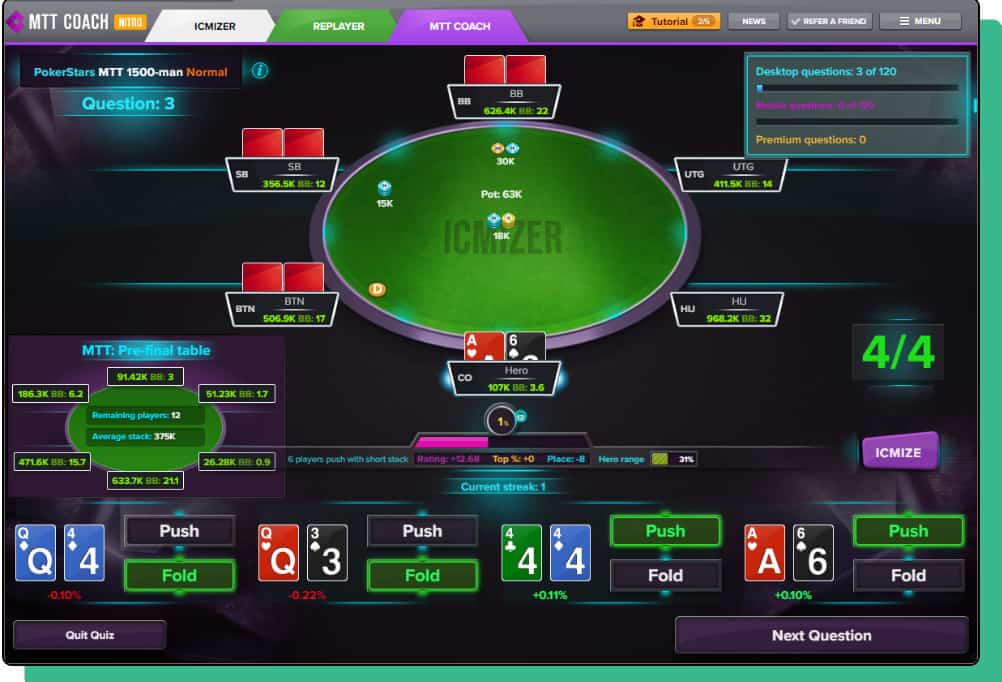
Als Trainingssoftware für das oben genannte ICM-Modell empfehlen wir Ihnen den ICMIZER. Der ICMIZER bietet Ihnen für verschiedenste Formate ein ausgiebiges Training an. Das Training unterstützt nahezu alle relevanten Pokeranbieter und deckt alle relevanten Situationen in Turnieren oder Sit & Go-Spielen ab, wenn Sie vor All-In-Entscheidungen stehen.
Poker Mathematik Buch
Neben Trainingssoftware kann es sich auch sehr lohnen, Pokerbücher zu lesen. Grundsätzlich gilt: Sie sollten neben dem Spielen immer auch Poker lernen. Es gibt zwar einige Bücher, die sich stärker auf die Pokermathematik fokussieren, wie Essential Poker Math, jedoch empfehlen wir Ihnen prinzipiell Bücher, die das große Ganze behandeln.
Auch, wenn diese Bücher inzwischen einige Jahre alt sind, gelten die Werke von Dan Harrington als Goldstandard – sowohl seine Cash- als auch seine Turnierbücher.
Ein ebenfalls sehr hilfreiches Werk mit viel Fokus auf Poker-Mathematik ist die mehrteilige Serie Erfolg bei Pokerturnieren von Eric Lynch, Jon van Fleet und Jon Turner. Diese Bücher behandeln sowohl die Theorie als auch praktische Beispiele und Übungen.
Nur wer die Pokermathematik beherrscht, pokert erfolgreich!
Die Hände zu kennen, die Regeln zu beherrschen oder zu glauben, gut bluffen zu können, macht Sie beim Pokerspiel nicht zum Gewinner. Wenn Sie erfolgreich Poker spielen möchten, müssen Sie die Pokermathematik beherrschen. Sicher kennen Sie den Spruch, dass Poker leicht zu erlernen, aber schwer zu meistern ist. Und “meistern“ meint hauptsächlich die Zahlen.
Poker entpuppt sich auf den zweiten Blick als ein äußerst komplexes Spiel mit einer tiefgründigen Mathematik, die selbst den klügsten Köpfen viel Fleiß und Übung abverlangt. Auch, wenn Sie nach Jahren glauben, ein guter Pokerspieler zu sein und sich mit Ihren Gewinnen einen Restaurantbesuch leisten können, bleibt immer noch viel Luft nach oben.
Spielen und Lernen sollten beim Pokerspiel stets Hand in Hand gehen. Wenn Sie nur spielen, ohne zu lernen, laufen Sie Gefahr, sich schlechte Angewohnheiten anzueignen – selbst, wenn Sie das Spiel eigentlich in- und auswendig kennen.


















